Домен Фурье - правильно ли я понял мою теорию / терминологию?
С точки зрения изображений.
Преобразование Фурье преобразует пространственную в частотную (Фурье) область. Значение DC = среднее значение синусоид (синусоид), F(0,0) и средняя яркость / уровень градации изображения. У Фурье есть комплексный выходной сигнал.... вы можете получить [амплитуду и фазу] или [реальный и мнимый] выходы.
Чего я не понимаю, так это то, что вывод комплексного числа на самом деле представляет, когда вы делаете FFT? Я знаю, что изображение в области Фурье является суммой взвешенных синусоидальных волн, но что на самом деле означает результат.
Что такое пространственная частота? Когда я смотрю на определения, это говорит о скорости изменения значений пикселей. Что это значит?
3 ответа
Таким образом, вы можете визуализировать ее лучше, если вы параметризуете информацию комплексного числа в величину и значение фазы, она отражает величину частотного компонента, а фаза дает вам положение компонента в изображении.
Пространственная частота обычно относится к изменению значения интенсивности при перемещении по пикселям. Таким образом, край вашего изображения будет иметь высокую пространственную частоту из-за резкого изменения значений пикселей
Выходы комплексного числа дают вам величину и фазу различных базисных векторов / сигналов Фурье.
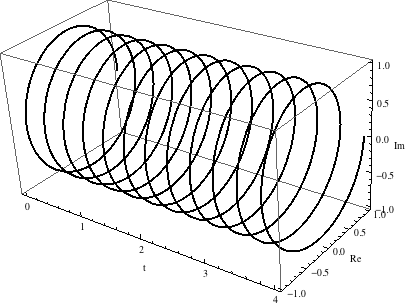
В случае одномерного сигнала, например звука, эти базисные векторы являются сложными синусоидами, вращающимися вокруг единичного круга с разными (пространственными) частотами (которые являются целыми кратными основной частоты) с течением времени.
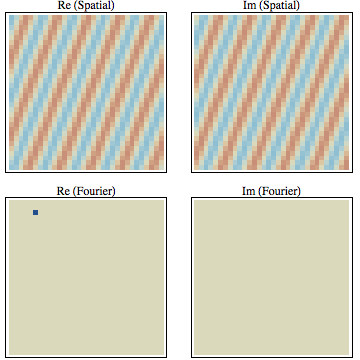
В случае изображения базисными векторами являются двумерные (комплексные) плоские волны. Теперь компоненты также могут иметь разные направления. Таким образом, каждый пиксель в пространстве Фурье равен определенной комбинации направления и частоты. Проще говоря, направление и частота плоской волны в пространственной области, начинающейся в верхнем левом углу, заканчиваются одним полным периодом к тому времени, когда он достигает положения соответствующего пикселя области Фурье (самым прямым способом).
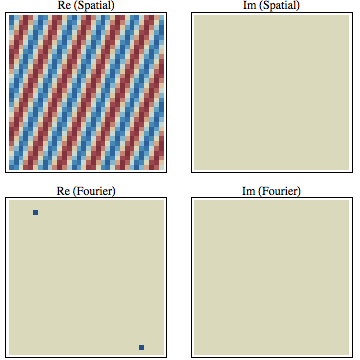
Для моделирования действительной синусоиды или плоской волны два комплексных базисных вектора с частотами одинаковой величины, но с отрицательной частотой накладываются друг на друга, так что их мнимые части сокращаются.
Результат сложный, потому что синусоиды могут быть смесью ортогональных синусоидальных волн и косинусоидальных волн, а комплексное число - математически хороший способ представить эту комбинацию синус + косинус.
Подумайте о заборчике с равномерно расположенными пикетами по всему изображению. Пространственная частота - это количество пикетов по изображению (по горизонтали или по вертикали). Сдвиньте забор на изображении на половину пикета (одна четверть периодичности), и забор может переключаться между тем, чтобы больше походить на синусоидальную волну, а не на косинусную волну. Представление комплексного числа будет вращаться.
Что это значит? Удивительная теория Фурье заключается в том, что каждое изображение (за исключением некоторых извращенных математических конструкций) может быть представлено или деконструировано в группу ортогональных синусоид пространственной частоты. (Каждое изображение. Не только изображения заборов!) После преобразования изображений в частоты вы можете выполнять на них всевозможные DSP, аналогичные обработке звука или фильтрации, а затем конвертировать обратно.