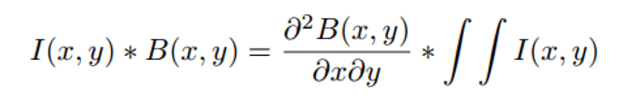Аппроксимации коробчатых фильтров для ориентированных фильтров Габора
В настоящее время я читаю эту статью: Аппроксимации в модели HMAX, меня особенно интересует аппроксимация фильтра Габора с помощью фильтров Бокса.
В прошлом году я разработал генератор синтетических отпечатков пальцев (некоторые из них вы можете увидеть здесь. Как свертывать изображение с помощью различных фильтров Габора, отрегулированных в соответствии с локальной ориентацией и плотностью с помощью БПФ?).
Но самый большой недостаток в генераторе - это время, которое требуется для применения фильтра Габора. Я изучал, как реализовать отдельную версию фильтра, но ужасно потерпел неудачу, так как математика не моя сильная сторона. Теперь это кажется лучше для моих нужд, чем разделимый фильтр, так как он кажется быстрее и результаты кажутся достаточно хорошими для того, что мне нужно. Но я не понимаю, как реализовать коробочную фильтрацию для gabor из уравнения в этой статье.
Это идет следующим образом:
В этом разделе мы попытаемся выполнить грубое приближение фильтра, чтобы добиться значительно более высокой эффективности. В настоящее время слой S1 в модели состоит из простых линейных детекторов, которые моделируются с использованием ориентированных фильтров Габора. Однако ориентированные линии могут быть представлены с использованием гораздо более простых представленных, таких как прямоугольные фильтры, как показано на рисунке 5. Эти фильтры имеют очень редкие производные, что позволяет нам достаточно эффективно вычислять свертку. Свертка изображения с фильтрами B(x, y) может быть эффективно вычислена с использованием производных фильтра следующим образом.
Вторая производная от прямоугольного фильтра состоит только из импульсов и поэтому должна оцениваться только в четырех точках для каждой позиции на изображении. Интегральное изображение также может быть эффективно рассчитано с использованием алгоритма однократного прохождения, как описано в [5, 1]. Стоимость свертки с использованием этого приближения составляет O(N2c), c=4. В отличие от других приближений, вычислительные затраты вообще не зависят от размера фильтра!
Каковы эти условия? Это интеграл от изображения? Прошу прощения, если это как супер базовые вещи, которые я спрашиваю, но я, честно говоря, понятия не имею:(.
1 ответ
Уравнение rhs в вашем вопросе - это бесконечно малое описание свертки - у вас есть оператор свертки " * ", который применяется к 2D-поддиапазону изображения - этот 2-мерный поддиапазон выражается как 2D-интеграл. Дискретное описание аналогично, но с двумерным поддиапазоном, выраженным оператором суммирования с использованием сигма-нотации "Σ". вместо двумерного интеграла он применяется как "ΣΣ" (я не знаю, как поставить здесь математическую запись).
Наивная реализация свертки использует 2 цикла - в каждой точке изображения вы суммируете значения ядра, умноженные на эту точку и соседние точки -
P (x + c / 2) = P (x) * C (1) + P (x + 1) * C (2)... + P (x + c) * C (c) (c - размер ядра). Процесс похож на длинное умножение или полином с умножением полинома.
В основном свертка может быть применена по-разному, один путь - прямой (суммирование) или путем преобразования в другие пространства (быстрое преобразование Фурье) - теорема о свертке.
Время БПФ - O (NlogN). использование FFT для свертки эффективно, если размер ядра большой. В противном случае, если размер ядра мал: O(c)
Также вы можете параллельно свернуть (через CUDA, Open-MP, и т.д...)