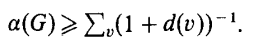Независимое множество в графе
Как вы знаете, нахождение максимального независимого набора - это NP. Есть ли алгоритм, чтобы узнать, имеет ли данный граф Независимый набор по крайней мере k вершин? Обратите внимание, что мы не хотим его найти. Мы просто хотим выяснить, существует ли такая вещь.
1 ответ
Цитируя Википедию:
В задаче решения с независимым набором входные данные представляют собой неориентированный граф и число k, а выходные данные представляют собой булево значение: true, если граф содержит независимый набор размера k, и false в противном случае.
Эта проблема является NP-полной. Ваша задача задает тот же вопрос, просто по-разному сформулированный, потому что граф имеет независимый набор по крайней мере из k вершин тогда и только тогда, когда у него есть независимый набор из ровно k вершин.
Это означает, что ваша проблема тоже NP-полная.
Существует хорошая нижняя граница размера максимального независимого множества ("число независимости графа" обозначается альфа),
где d(v) - степень вершины v, а сумма ведется по всем вершинам простого графа G. Она была независимо открыта Вей и Каро (я нашел ее в "Нижних оценках числа независимости в терминах степеней "Дж. Р. Григгса) и существуют другие нижние оценки для различных типов графов.
Это означает, что максимальное независимое множество будет иметь не менее k вершин с k, заданным этой нижней границей.